6. Algorithm description: ocean
6.1 Strategy
Let us assume that from the Main core, we have received an N x N worth of gas-corrected pixels, \(\rho_\lambda\)L1B along with the geolocation, cloud mask results (assuming the entire N x N box is ocean), and the ancillary wind speed information. The mechanics of the ocean algorithm are illustrated in figure 6-1. The basic strategy of the dark target aerosol retrieval over the ocean (DT-O) is described in in Tanré et al. [1997], Levy et al. [2003], Remer et al. [2005] with the dynamic wind speed addition explained in Kleidman et al. [2012]. It follows the DT strategy presented in Section 2.2, in that one fine “f” and one coarse “c” aerosol model can be combined with FMW ( \(\eta\) ) to represent the ambient aerosol properties and TOA spectral reflectance (Eq. 2-27.; rewritten here),
![]() Equation 6-1
Equation 6-1
Spectral reflectance from the LUT is compared with MODIS-measured spectral reflectance to find the ‘best’ (least-squares) fit. The best fit, or an ‘average’ of a set of the best fits is used as the solution to the inversion. Although the core inversion remains similar to the process described in Tanré, et al. (1997), and updates including sediment masking and the special handling of heavy dust including dust retrievals over glint included in ATBD-09, minor updates to masking of clouds and the inclusions of multiple wind speed look-up tables are new. In this section, we describe the over-ocean LUTs, the cloud masking and pixel selection logic, the retrieval strategy details, and over-ocean product description.
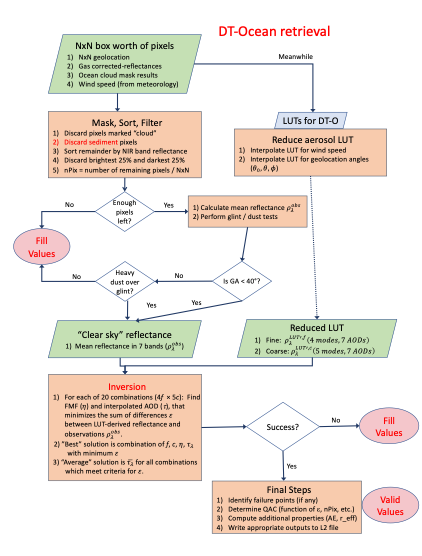
6.2 LUTs for DT Ocean
6.2.1 Aerosol Models
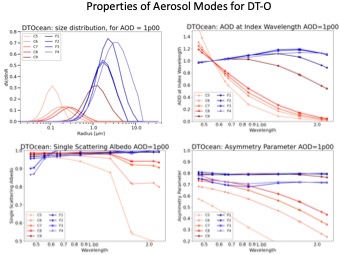
The aerosol optical models for DT-O are derived mainly from data gleaned from sun/sky photometers (e.g. AERONET; Holben et al., [1998]), and from analysis of errors in the products from previous versions of the algorithm. For DT in general, there are four fine modes and five coarse modes, with spectral refractive indices and lognormal size parameters computed via a Mie code. Table 6 -1 to Table 6-4 describe spectral properties of the aerosol modes for the exact MODIS wavelengths (Table 3-2.), for unit AOD =1.0 (at 0.55 mm). Other sensors will have similar spectral properties, although different exact values at their respective wavelengths. Figure 6-2 illustrates the properties of 4 fine and 5 coarse modes for the DT-O, plotted at MODIS and VIIRS wavelengths, computed for AOD = 1.0 at 0.55 μm.
|
F |
\(\lambda\) = blue, green, red, NIR |
\(\lambda\) =NIR1 |
\(\lambda\) =SWIR1 |
\(\lambda\) =SWIR2 |
rg |
\(\sigma\) |
reff |
Comments |
|---|---|---|---|---|---|---|---|---|
|
1 |
1.45-0.0035i |
1.45-0.0035i |
1.43-0.01i |
1.40-0.005i |
0.07 |
0.40 |
0.10 |
Water Soluble |
|
2 |
1.45-0.0035i |
1.45-0.0035i |
1.43-0.01i |
1.40-0.005i |
0.06 |
0.60 |
0.15 |
Water Soluble |
|
3 |
1.40-0.0020i |
1.40-0.0020i |
1.39-0.005i |
1.36-0.003i |
0.08 |
0.60 |
0.20 |
Water Soluble + humidity |
|
4 |
1.40-0.0020i |
1.40-0.0020i |
1.39-0.005i |
1.36-0.003i |
0.10 |
0.60 |
0.25 |
Water Soluble + humidity |
|
C |
\(\lambda\) =blue, green, red, NIR |
\(\lambda\) =NIR1 |
\(\lambda\) =SWIR1 |
\(\lambda\) =SWIR2 |
rg |
\(\sigma\) |
reff |
Comments |
|---|---|---|---|---|---|---|---|---|
|
5 |
1.35-0.001i |
1.35-0.001i |
1.35-0.001i |
0.40 |
0.60 |
0.98 |
Wet sea salt type |
|
|
6 |
1.35-0.001i |
1.35-0.001i |
1.35-0.001i |
1.35-0.001i |
0.60 |
0.60 |
1.48 |
Wet sea salt type |
|
7 |
1.35-0.001i |
1.35-0.001i |
1.35-0.001i |
1.35-0.001i |
0.80 |
0.60 |
1.98 |
Wet sea salt type |
|
8 |
1.53-0.003i (blue) 1.53-0.001i (green) 1.53-0.000i (red, NIR) |
1.46-0.000i |
1.46-0.001i |
1.46-0.000i |
0.60 |
0.60 |
1.48 |
Dust-like type |
|
9 |
1.53-0.003i (blue) 1.53-0.001i (green) 1.53-0.000i (red, NIR) |
1.46-0.000i |
1.46-0.001i |
1.46-0.000i |
0.50 |
0.80 |
2.50 |
Dust-like type
|
|
\(\lambda\) (\(\mu\)m) Mode |
0.466 |
0.554 |
0.645 |
0.857 |
1.241 |
1.628 |
2.113 |
AE |
0.86 0.55 |
2.11 0.86 |
|---|---|---|---|---|---|---|---|---|---|---|
|
1 F |
1.539 |
1 |
0.66 |
0.285 |
0.086 |
0.047 |
0.016 |
|
2.877 |
3.183 |
|
2 F |
1.305 |
1 |
0.764 |
0.426 |
0.17 |
0.081 |
0.03 |
|
1.957 |
2.927 |
|
3 F |
1.247 |
1 |
0.796 |
0.481 |
0.213 |
0.105 |
0.042 |
|
1.677 |
2.696 |
|
4 F |
1.187 |
1 |
0.832 |
0.547 |
0.269 |
0.14 |
0.06 |
|
1.385 |
2.449 |
|
5 C |
0.966 |
1 |
1.022 |
1.026 |
0.918 |
0.764 |
0.586 |
|
-0.058 |
0.619 |
|
6 C |
0.967 |
1 |
1.033 |
1.093 |
1.118 |
1.058 |
0.927 |
|
-0.204 |
0.182 |
|
7 C |
0.977 |
1 |
1.026 |
1.087 |
1.166 |
1.179 |
1.124 |
|
-0.191 |
-0.037 |
|
8 C |
0.977 |
1 |
1.026 |
1.087 |
1.185 |
1.192 |
1.127 |
|
-0.19 |
-0.04 |
|
9 C |
0.982 |
1 |
1.019 |
1.059 |
1.118 |
1.137 |
1.126 |
|
-0.131 |
-0.069 |
|
\(\lambda\) (\(\mu\)m) Mode |
0.466 |
0.554 |
0.645 |
0.857 |
1.241 |
1.628 |
2.113 |
|---|---|---|---|---|---|---|---|
|
1 F |
0.974 |
0.968 |
0.961 |
0.94 |
0.879 |
0.541 |
0.499 |
|
2 F |
0.978 |
0.977 |
0.976 |
0.97 |
0.956 |
0.817 |
0.822 |
|
3 F |
0.987 |
0.986 |
0.986 |
0.984 |
0.978 |
0.921 |
0.916 |
|
4 F |
0.986 |
0.987 |
0.987 |
0.985 |
0.982 |
0.94 |
0.941 |
|
5 C |
0.978 |
0.982 |
0.985 |
0.989 |
0.991 |
0.992 |
0.993 |
|
6 C |
0.966 |
0.972 |
0.976 |
0.983 |
0.988 |
0.991 |
0.992 |
|
7 C |
0.955 |
0.962 |
0.967 |
0.976 |
0.984 |
0.988 |
0.99 |
|
8 C |
0.901 |
0.967 |
1 |
1 |
1 |
0.99 |
1 |
|
9 C |
0.867 |
0.953 |
1 |
1 |
1 |
0.983 |
1 |
|
\(\lambda\) (\(\mu\)m) Mode |
0.466 |
0.554 |
0.645 |
0.857 |
1.241 |
1.628 |
2.113 |
|---|---|---|---|---|---|---|---|
|
1 F |
0.576 |
0.511 |
0.447 |
0.321 |
0.178 |
0.105 |
0.063 |
|
2 F |
0.683 |
0.66 |
0.635 |
0.575 |
0.468 |
0.369 |
0.265 |
|
3 F |
0.735 |
0.718 |
0.699 |
0.651 |
0.559 |
0.472 |
0.372 |
|
4 F |
0.751 |
0.74 |
0.726 |
0.69 |
0.618 |
0.546 |
0.458 |
|
5 C |
0.785 |
0.786 |
0.789 |
0.794 |
0.795 |
0.787 |
0.769 |
|
6 C |
0.795 |
0.788 |
0.786 |
0.787 |
0.794 |
0.796 |
0.792 |
|
7 C |
0.81 |
0.8 |
0.793 |
0.786 |
0.788 |
0.794 |
0.796 |
|
8 C |
0.753 |
0.72 |
0.697 |
0.679 |
0.713 |
0.72 |
0.719 |
|
9 C |
0.78 |
0.746 |
0.723 |
0.706 |
0.722 |
0.722 |
0.715 |
The DT-O LUT employs the Ahmad and Fraser (1981) vector radiative transfer (AFRT) code to simulate TOA reflectance for a coupled ocean/atmosphere. AFRT includes toggles for whether to include polarization (turned on), trace gas coupling (turned off) and pseudospherical atmosphere (turned on). AFRT includes an internal Mie code (for calculating scattering properties of spherical particles) but can be set up to use external calculations of scattering properties (if non-spherical). For spherical modes 1F to 9C all Mie calculations are performed internally.
6.2.2. Reflectance-versus-Aerosol LUT
The spectral reflectance at the satellite level is the coupled combination of radiation from the surface and the atmosphere. The ocean surface calculation includes sun glint reflection off the surface waves [Cox and Munk, 1954], reflection by foam and whitecaps [Koepke, 1984] and Lambertian reflectance from underwater scattering (sediments, chlorophyll, etc). The LUT includes simulations for four wind speeds, 2 m/s, 6 m/s, 10 m/s, and 14 m/s, having foam fractions of 0.01%, 0.16%, 1% and 3%, respectively (e.g. Monahan and Muircheartaigh, [1980] ). Zero water leaving radiance is assumed for all compared wavelengths, except for the green, where a fixed reflectance of 0.005 is used. The atmospheric contribution includes multiple scattering by gas and aerosol, as well as reflection of the atmosphere by the sea surface. Central wavelengths, Rayleigh optical depths and molecular depolarization factors (also known as King factors) are prescribed in the AFRT, based on the exact characteristics of the sensor’s wavelength bands.
Thus, TOA spectral reflectance is computed for each of the nine spherical aerosol models (combined with Rayleigh and surface) described in the Table 6‑1. Six values of total aerosol loading (AOD at 0.55 μm, denoted as t number of AOD) are considered for each mode, ranging from a pure molecular (Rayleigh) atmosphere (\(\tau\) 0.0) to a highly turbid atmosphere (\(\tau\) = 3.0), with intermediate values of 0.2, 0.5, 1.0 and 2.0. For each model and aerosol optical depth at 0.55 μm, the associated aerosol optical depths are stored for all the sensor’s seven wavelengths, including the blue, which is not used in the least squares fit to spectral reflectance. Also stored are aerosol optical depth values for the sensor’s green channel, which may or may not be the same as the reference wavelength of 0.55 µm. Computations are performed for combinations of 11 solar zenith angles (6°, 12°, 24°, 36°, 48°, 54°, 60°, 66°, 72°, 78° and 84°), 16 satellite view zenith angles (0° to 72°, increments of 6°) and 16 relative sun/satellite azimuth angles (0° to 180°, increments of 12°) for a total of 2816 angular combinations. Again, note that scattering and LUT calculations are specific for a given sensor’s wavelength band, however always normalized to AOD = 1.0 at 0.55 μm. Also note that for sensors that do not include a particular band (e.g., no NIR1 on ABI or AHI), placeholders are included so that the LUT will always be indexed for 7 wavelengths. Let us denote the spectral reflectance in the LUT as \(\rho_\lambda\)LUT(v, j, \(\tau\),\(\theta\)0,\(\theta\),\(\phi)\) where v, j, \(\tau\),\(\theta\)0,\(\theta\),\(\phi\) are indices for windspeed, aerosol model, aerosol loading (defined by AOD at 0.55 mm), and angles. During the retrieval, this LUT spectral reflectance is interpolated to represent the actual wind speed (provided by ancillary information) and angles.
6.3 Selection of Pixels: Cloud, Glint and Sediment Masking
6.3.1 Masking Overview:
The masking of clouds and sediments and the selection of pixels are described in Remer et al., [2005] and Levy et al., [2013]. Much attention has been paid in the algorithm to the difficult task of separating usable “clear” pixels from cloudy or cloud contaminated pixels [Remer et al., 2012]. Most standard cloud masks, e.g. the Continuity MODIS-VIIRS cloud mask [Frey et al., 2020] includes using the brightness in the visible channels to identify clouds. This procedure can incorrectly identify heavy aerosol as ‘cloudy’, and will thereby miss retrieving significant aerosol events over ocean. On the other hand, relying on IR-tests alone permits low altitude, warm clouds to escape and be misidentified as 'clear', introducing cloud contamination in the aerosol products. Thus, our cloud mask over ocean combines spatial variability tests (e.g. Martins et al. [2002]) along with tests of brightness in visible and infrared channels. Appendix 3.1.1 describes the cloud mask over ocean. Underwater sediments have proved to be a problem in shallow water (near coastlines) as the sediments can easily have land-like surface properties. Thus, the sediment mask is used in addition to the cloud mask, using all available wavelength described in Li et al. [2003] (Appendix 3.1.2).
The algorithm sorts the remaining pixels that have evaded all the cloud masks and the sediment mask according to their \((rho\) L1B NIR value, discards the darkest and brightest 25%, and thereby leaves the middle 50% of the data. The filter is used to eliminate residual cloud contamination, cloud shadows, or other unusual extreme conditions in the box. Because the ocean cloud mask and the ocean surface are expected to be less problematic than their counterparts over land, the filter is less restrictive than the one used in the land retrieval. A minimum number of pixels remaining after masking and filtering is needed for the algorithm to continue. The algorithm also requires a minimum of 5% pixels at NIR channel over ocean with at least 10% pixels distributed over the other five channels. If the minimum number of pixels is not met, no retrieval is attempted, and fill values are given for the aerosol products in the retrieval box. If the minimum is met, the mean reflectance and standard deviation are calculated for the remaining 'good' pixels at the pertinent wavelengths. Let us denote the vector of observed mean spectral reflectance as \(\tau\)\(\rho\)obs. By this point it is assumed to be suitable for inversion, meaning free of clouds, cloud edges, and sediments.
6.3.2 Ocean Glint and Internal Consistency:
The ocean algorithm was designed to retrieve only over dark ocean, (i.e. away from glint). There is a special case when we retrieve over glint, and that is described below. The algorithm calculates the glint angle, which denotes the angle of reflection, compared with the specular reflection angle. The glint angle was defined via Equ 23B. Note that Fresnel reflection corresponds to
= 0. If
> 40˚, we can avoid glint contamination and proceed with the retrieval. The algorithm performs several consistencies checks of the spectral reflectances. Depending on the outcome of these consistency checks, the algorithm may either declare the reflectances to be beyond the range necessary for a successful inversion and exit the procedure or continue onto the inversion after assigning a quality assurance ‘confidence’ flag (QAC) to each wavelength (See Section 5.2).
Following Tanré et al. [1996], we know that the measured multi-channel spectral radiance , spanning visible through SWIR (green, red, NIR, SWIR2), contains almost three pieces of independent information about the aerosol loading and size properties. With assumptions that limit the choices of possible aerosol types to those in Table 6-1, the algorithm can derive three parameters: the total AOD defined at 0.55 mm, (
), the ‘reflectance weighting parameter’ (the over-ocean definition of Fine Model Weighting -
), and the choice of which combination of ‘fine’ (f) and single ‘coarse’ (c) aerosol modes that lead to the solution. The combination of
and mode choices translate to the ‘‘effective radius’ (re), which is the ratio of the 3rd and 2nd moments of the aerosol size distribution.
We note that the retrieval of is determined based on reflectance weighting, but that by knowing how the spectral dependence of reflectance is related to each model’s AOD within the LUT (indexed at 0.55 mm), we also uniquely derive Fine Mode Weighting in terms of AOD,
. This means that in addition to total AOD at any wavelength,
, we can also estimate the fine and coarse models’ contributions to total AOD at 0.55 mm (
and
). Since we know the spectral extinction of each model, we can also report fine and coarse AOD any wavelength (
and
).
The trick is to determine “which” fine and coarse models represent the best solutions. The first step is to interpolate the LUT, removing the dependencies of the LUT reflectance on wind speed and angles, resulting in . Models j are assumed to be split into four fine modes f=1,4 and c=5,9. The difficulty is in determining which of the (4 ´ 5 = 20) twenty combinations of fine and coarse modes and their relative optical contributions
and
that best mimics the observed spectral reflectance
. The retrieval proceeds via iteration. Each combination of f and c is tested (e.g.
and
, with simultaneous interpolation between values of
(between 0.0 and 1.0) and aerosol loading values (indexed by t) within the LUT. The result for each combination
Eq. 6‑2
where is a weighted average reflectance of an atmosphere with a pure fine mode 'f' and optical thickness
and the reflectance of an atmosphere with a pure coarse mode 'c' also with the same
. Thus, the inversion finds the pair of
and
that minimizes the ‘fitting error’ (
) defined as
Eq. 6‑3
where is the number of pertinent wavelengths for the retrieval. Note that the blue channel is never used in the retrieval to avoid uncertainty in ocean color, Therefore, the maximum value of
is six, but specific sensors may use fewer pertinent wavelengths.
is the sum of good pixels at wavelength
,
is the measured MODIS reflectance at wavelength
,
is the reflectance contributed by Rayleigh scattering, and
is calculated from the combination of modes in the LUT and defined by Eq. 6‑2. The 0.01 is to prevent a division by zero for the longer wavelengths under clean conditions [Tanré et al. 1997]. The inversion requires
to exactly fit the observations at that wavelength and then finds the best fits to the other five or fewer wavelengths via Eq. 6‑3. The NIR channel was chosen to be the primary wavelength because it is expected to be less affected by variability in water leaving radiances than the shorter wavelengths, yet still exhibit a strong aerosol signal, even for aerosols dominated by the fine mode By emphasizing accuracy in this channel variability in chlorophyll will have negligible effect on the optical thickness retrieval and minimal effect on
. For each combination (f, c,
and
) one can use the LUT to infer a variety of parameters, including spectral optical depth, fine-mode AOD, coarse-mode AOD, effective radius, spectral flux, mass concentration, etc.
This iterative fitting process occurs for each of the twenty fine/coarse mode combinations, which are then sorted according to values of e. The combination of modes with accompanying and
, with the minimum
, is known as the ‘best’ solution. Let us denote this ‘best’ solution combination as
,
and
, and we record the inferred ‘best’ parameters associated this combination (spectral AOD, fine/coarse AOD, effective radius, etc.). A study exploring the sensitivity of the basic retrieval to perturbations in calibration, surface assumptions, glint and to situations not well-represented in the LUT. The results of this study are given in Tanré et al. [1997].
This ‘best’ solution might be a poor solution (large fitting error), or it may be one of multiple “good” solutions that have similar fitting error less than a threshold (currently set as e < 3.7%). Therefore, the DT retrieval also calculates a more robust ‘average’ solution and
. How the ‘avg’ is calculated, depends on the number of good solutions. If the ‘best’ solution is the only good one, then all ‘avg’ are set to the same values as the ‘best’. If there are at least two good solutions, then ‘avg’ is the simple average of those. However, if there are no good solutions (all combinations have e ≥ 3.7%), then the top three combinations are used to calculate a weight-based ‘avg’, where the weights are based on a modified epsilon, e.g
. Regardless of the method used for calculating the average solutions, we record the derived spectral AOD, fine/coarse AOD, effective radius, etcetera.
4.4 Retrieval Algorithm
The ocean inversion procedure described in ATBD-96, Levy et al., (2003) and Remer et al., (2005) remains the same for the C6-O algorithm. Following Tanré et al. (1996), we know that the MODIS-measured spectral radiance (0.55 – 2.13 µm) contains almost three pieces of independent information about the aerosol loading and size properties. With some assumptions, the algorithm can derive three parameters: the τ at one wavelength τtot0.55 , the ‘reflectance weighting parameter’ (the over-ocean definition of Fine Weighting - η) at one wavelength (ηλ=0.55 ) and the ‘effective radius’ (re), which is the ratio of the 3rd and 2nd moments of the aerosol size distribution. The effective radius is represented by choosing a single ‘fine’ (f) and single ‘coarse’ (c) aerosol mode for weighting with the η parameter. The inversion is based on the look-up table (LUT) of four fine modes and five coarse modes (Table 2). Although the LUT is defined in terms of a single wavelength of optical thickness, the parameters of each of the single mode models define a unique spectral dependence for that model, which is applied to the retrieved value of 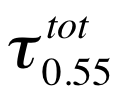 , to determine optical thickness at the other reported wavelengths.
, to determine optical thickness at the other reported wavelengths.
The retrieval requires a single fine mode and a single coarse mode. The difficulty is in determining which of the (4 x 5 =) twenty combinations of fine and coarse modes and their relative optical contributions that best mimics the MODIS-observed spectral reflectance. To accomplish this the reflectance from each mode is combined using η as the weighting parameter,
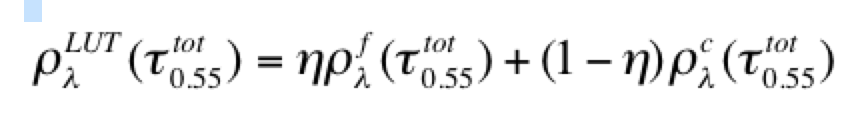 (26)
(26)
where 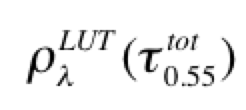 is a weighted average reflectance of an atmosphere with a pure fine mode 'f' and optical thickness
is a weighted average reflectance of an atmosphere with a pure fine mode 'f' and optical thickness 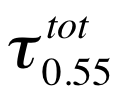 and the reflectance of an atmosphere with a pure coarse mode 'c' also with the same
and the reflectance of an atmosphere with a pure coarse mode 'c' also with the same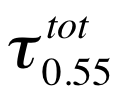 . For each of the twenty combinations of one fine mode and one coarse mode, the inversion finds the pair of
. For each of the twenty combinations of one fine mode and one coarse mode, the inversion finds the pair of 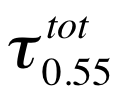 and η0.55 that minimizes the ‘fitting error’ (ε) defined as
and η0.55 that minimizes the ‘fitting error’ (ε) defined as
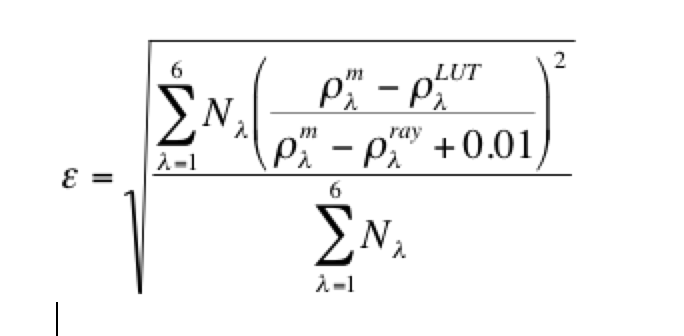 (27)
(27)
where Nλ is the sum of good pixels at wavelength λ, ρλm is the measured MODIS reflectance at wavelength λ, ρλray is the reflectance contributed by Rayleigh scattering, and ρλLUT is calculated from the combination of modes in the look-up table and defined by Equation (26). The 0.01 is to prevent a division by zero for the longer wavelengths under clean conditions (Tanré et al. 1997). Note the inclusion of the Rayleigh reflectance scattering in Equation (27), as compared with the formula in C4-O (Remer et al., 2005). The inversion requiresρ0.87 LUT to exactly fit the MODIS observations at that wavelength and then finds the best fits to the other five wavelengths via Equation (27). The 0.87 µm channel was chosen to be the primary wavelength because it is expected to be less affected by variability in water leaving radiances than the shorter wavelengths, yet still exhibit a strong aerosol signal, even for aerosols dominated by the fine mode. By emphasizing accuracy in this channel variability in chlorophyll will have negligible effect on the optical thickness retrieval and minimal effect on ηλ=0.55.
The twenty solutions are then sorted according to values of e. The ‘best’ solution is the combination of modes with accompanying 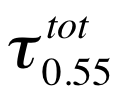 and ηλ=0.55 that minimizes ε. The solution may not be unique. The ‘average’ solution is the average of all solutions with ε< 3% or if no solution has ε < 3%, then the average of the 3 best solutions. Once the solutions are found, then the chosen combination of modes is the de facto derived aerosol model and a variety of parameters can be inferred from the chosen size distribution including spectral optical depth, effective radius, spectral flux, mass concentration, etc.
and ηλ=0.55 that minimizes ε. The solution may not be unique. The ‘average’ solution is the average of all solutions with ε< 3% or if no solution has ε < 3%, then the average of the 3 best solutions. Once the solutions are found, then the chosen combination of modes is the de facto derived aerosol model and a variety of parameters can be inferred from the chosen size distribution including spectral optical depth, effective radius, spectral flux, mass concentration, etc.
Final Checking
Before the final results are output, additional consistency checks are employed. In general, if the retrievedτ at 0.55 µm is greater than –0.01 and less than 5, then the results are output. Negative optical depths are rounded to exactly zero. There are exceptions and further checking for heavy dust retrievals made over the glint. The final QA-confidence flag may be adjusted during this final checking phase.
Special case: Heavy dust over glint.
If Θglint ≤ 40˚, a case where we normally do not retrieve, we check for heavy dust in the glint. We use a similar technique as before during the masking operations when we noted that heavy dust has a distinctive spectral signature because of light absorption at blue wavelengths. In the situation of identifying heavy dust over glint we designate all values of ρ0.47/ ρ0.65 < 0.95 to be heavy dust. If heavy dust is identified in the glint, the algorithm continues with the retrieval, although it sets QAC=0. This permits the retrieval, but prohibits the values from being included in the Level 3 statistics (Remer et al., 2005). If heavy dust is not identified in the glint, then the algorithm writes fill values to the aerosol product arrays and exits the procedure.
4.5 Algorithm Flow Chart
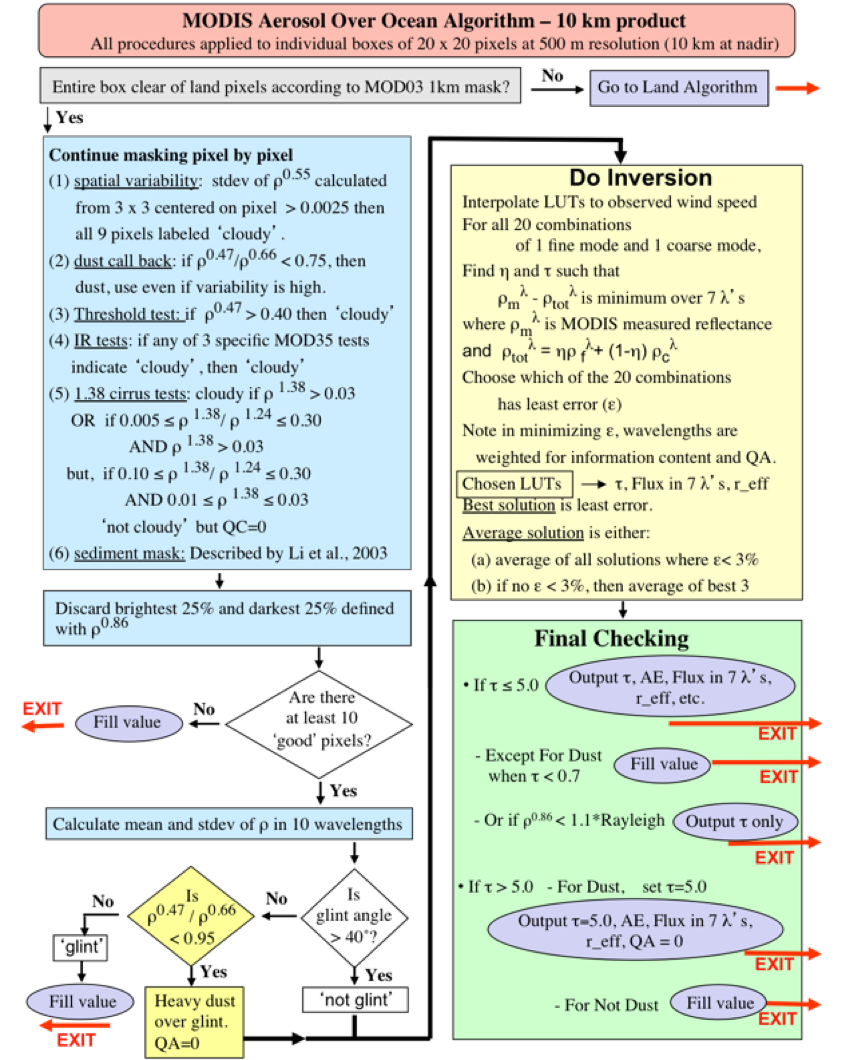
Figure 4: Flowchart of the over-ocean aerosol retrieval algorithm (adapted from Remer et al., 2005, updated for C6).
4.6 Retrieved ocean products
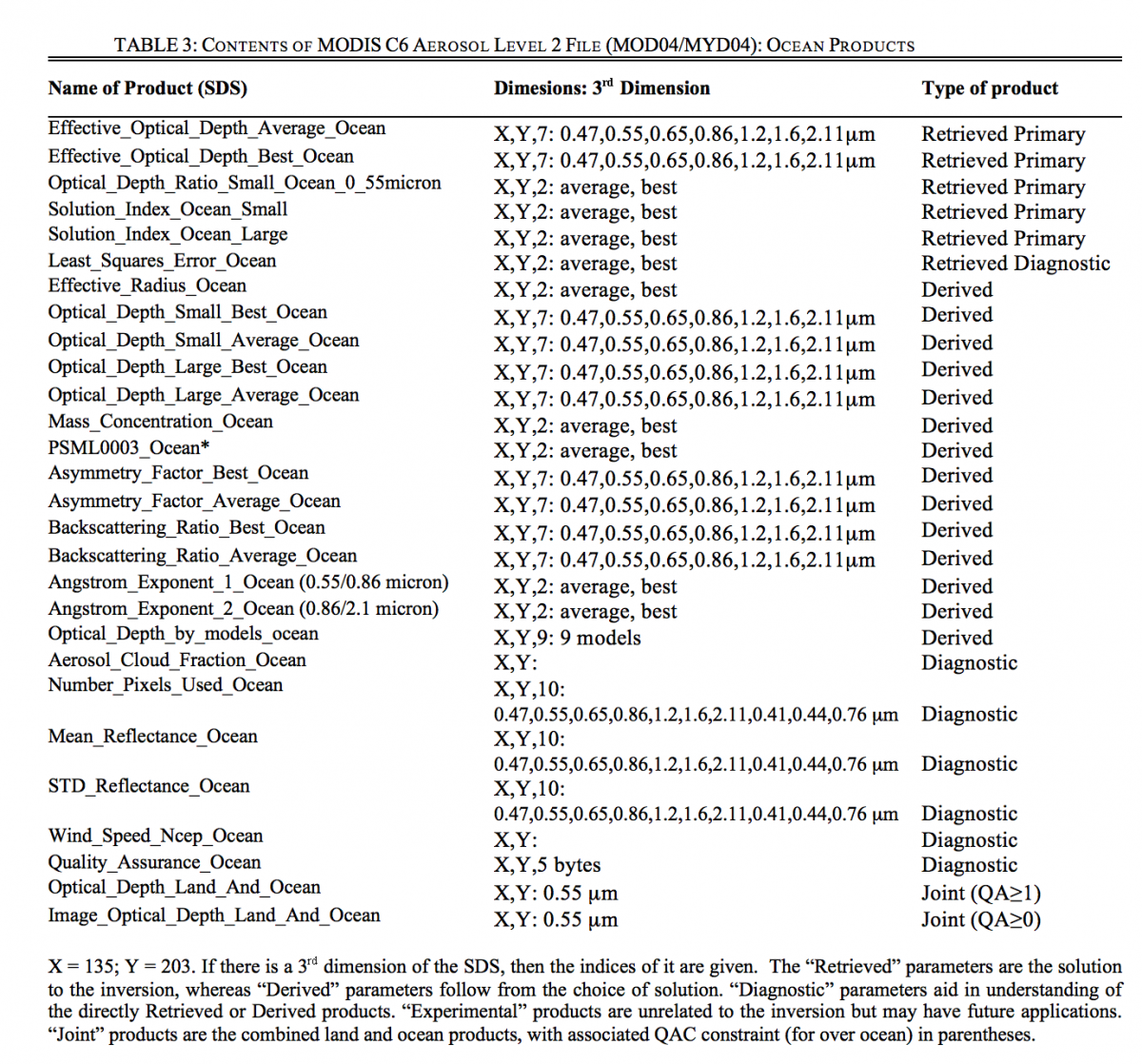
As discussed earlier, the primary retrieved products of the ocean algorithm are the total τ at 0.55 μm (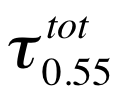 ), the Fine (Mode) Weighting (η or η 0.55 ) and which Fine (f) and which Coarse (c) modes were used in the retrieval. The fitting error (ε) of the simulated spectral reflectance is also retrieved. Both the ‘best’ and ‘average’ solutions are reported. From these primary products a number of other parameters can be easily derived. Examples include the effective radius (reff) of the combined size distribution, the spectral total, fine and coarse t values (
), the Fine (Mode) Weighting (η or η 0.55 ) and which Fine (f) and which Coarse (c) modes were used in the retrieval. The fitting error (ε) of the simulated spectral reflectance is also retrieved. Both the ‘best’ and ‘average’ solutions are reported. From these primary products a number of other parameters can be easily derived. Examples include the effective radius (reff) of the combined size distribution, the spectral total, fine and coarse t values (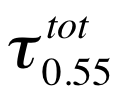 ,
,![]() and
and ![]() ), and a measure of the columnar aerosol mass concentration (MC). Table 3 lists the products retrieved and derived during the ocean retrieval algorithm. Details about the ‘Quality_Assurance_Ocean’ (QA) SDS are given in the Appendix. Note that a parameter’s type does not indicate whether a parameter should be used in a quantitative way. Each parameter must be independently validated via comparison with ground-truth measurements, where validation means that the product can be shown to be comparable with a set of ground-truth observations on a global scale, within some defined expected uncertainty. Prior to operational C6 processing, a testbed of 8 months of Aqua-MODIS granules were used to evaluate a few of the derived parameters. This provisional evaluation is described in Section 5. This ATBD document will be updated as the MODIS products are evaluated and reach validation status
), and a measure of the columnar aerosol mass concentration (MC). Table 3 lists the products retrieved and derived during the ocean retrieval algorithm. Details about the ‘Quality_Assurance_Ocean’ (QA) SDS are given in the Appendix. Note that a parameter’s type does not indicate whether a parameter should be used in a quantitative way. Each parameter must be independently validated via comparison with ground-truth measurements, where validation means that the product can be shown to be comparable with a set of ground-truth observations on a global scale, within some defined expected uncertainty. Prior to operational C6 processing, a testbed of 8 months of Aqua-MODIS granules were used to evaluate a few of the derived parameters. This provisional evaluation is described in Section 5. This ATBD document will be updated as the MODIS products are evaluated and reach validation status
Some of the ocean products are combined with products from land (discussed in the next section) as the Joint products. For τ , two joint products are reported, the ‘Optical_Depth_Land_And_Ocean’ and the ‘Image_Optical_Depth_Land_And_Ocean’. The first product is constrained by QAC whereas the “Image” product includes all QAC values in order to provide the most complete visulization of the AOD.
